I found myself asking this question after studying logarithms in school. Logs was always one of the less popular, less well-known topics at GCSE. So when people saw they were in the A-Level syllabus, many said "I hate logs" immediately after looking at the list of log rules.
But, logs are very similar to indices. And after solving several problems, I noticed - all numbers that are put into the log function are always positive. But why is this? Below, I try to summarise how I figured it out.
As I said earlier, we can think of logs like indices. The base of the log is the base of the exponent function. (Observe the result on the left).
Can the base be 0?
What if b = 0? Well, we know that 0 raised to any power is still 0. So, if b = 0, then it is impossible to determine y and so log base 0 is undefined.
So the base CANNOT be 0.
Now, what if the base is positive?
Now let's imagine the base is 1 i.e. b = 1. Again, just like last time, 1 raised to any power is just 1. E.g. 1 squared = 1, 1 cubed = 1, 1 to the power of -5 = 1. So again, no matter what value x takes, y cannot be determined.
This means the base cannot be 1. BUT - this is when I thought: what if the base is 1, and x = 1? Then, surely y = 0 because anything to the power 0 will give you 1?
But then I realised - log base 1 of 1 can, in fact, be any number. As we established earlier, 1 raised to any power gives 1. So, technically y can take ANY number. This is why b = 1 is undefined.
So the base CANNOT be 1.
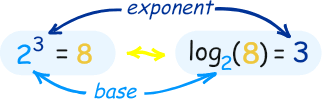
The base CAN be greater than 1 though, e.g. if b = 2, x = 8 and y = 3 (see diagram on the right). Similarly, the base can also be positive and less than 1 (i.e. between 0 and 1).
So, what happens when the base is negative?
If b < 0, this can pose some problems if e.g. y is not a positive integer. For example, if b = -4 and y = 1/2, then b^y = x is equal to the square root of -4. This wouldn't give us any real solutions!
So the base CANNOT be negative.
Putting together all 3 conclusions, we can say that the base of a logarithm can only be positive numbers excluding 1 i.e. 0 < b < 1 or b > 1.
What about the argument of the log?
So now, what about x? This is known as the argument of the log, as it is what we are inputting into the log function.
Well, we now know the base is always positive. So, this is the same as saying a positive number b to the power y is x.
And because b is positive, x will ALSO be positive no matter what y is. For example, take the example above with b = 2, x = 8 and y = 3. 2 cubed = 8 which is positive. But, if y was negative e.g. if y = -3, then x = 1/8 which is ALSO positive.
Let's quickly check if this is also the case for when y = 0. For any positive number b raised to the power 0, the result is 1, which is positive. Therefore, the result is true!
So overall, the base of a logarithm must be positive - and hence the argument of the log must also be positive.
Let's sum up the rules we've figured out!
1) Base of a log: can only be positive numbers that aren't equal to 1
2) Argument of a log: can only be positive numbers
3) Actual output of a log: can be positive OR negative numbers
Hope you've found this interesting and useful! I really enjoyed working this out and have also done other mathematical "explorations" - let me know if you want me to publish these on the website/see more posts like this in the future!
*If you enjoyed this, please subscribe on the website to join our community and get more insights just like this article.*
Looking for 1:1 tailored internship or work experience application help?
Sign up to Blaze Careers Tutoring, the world's first 1:1 careers tutoring site and get line-by-line help in CVs, cover letter and mock interview answer writing - all from someone in your dream industry/firm.
Boost your chances of landing that prestigious role among the thousands of other competitive candidates. Lessons offered in the investment banking industry (+ more to come!)
The logarithm function is well defined even when the base is a positive number less than 1. You might want to go back to the drawing board and figure out how! I would definitely want you to update your answer, however.